936. Peerless Trees

A peerless tree is a tree with no edge between two vertices of the same degree. Let $P(n)$$P(n)$ be the number of peerless trees on $n$$n$ unlabelled vertices.

There are six of these trees on seven unlabelled vertices, $P(7)=6$$P(7)=6$, shown below.

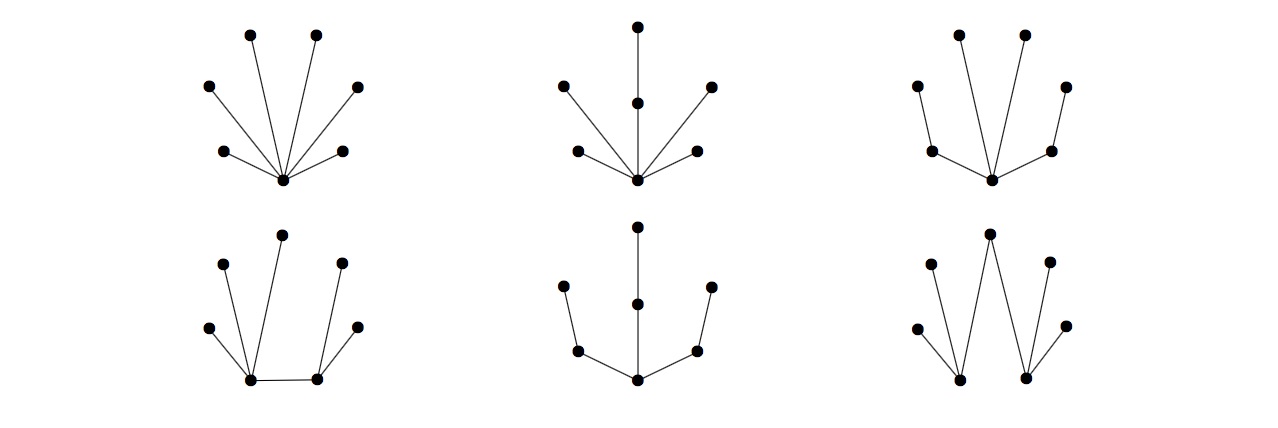
Define ${\displaystyle S(N)=\sum _{n=3}^{N}P(n)}$$\displaystyle S(N) = \sum_{n=3}^N P(n)$. You are given $S(10)=74$$S(10) = 74$.

Find $S(50)$$S(50)$.

936. 无同树 ¹

若一棵树满足：其中任意两个度数相同的节点之间没有连边，则称该树是一棵 无同树。记 $P(n)$$P(n)$ 为含 $n$$n$ 个节点的无标号无同树的数量。

例如 $P(7)=6$$P(7)=6$，下图展示了这 $6$$6$ 棵无标号无同树。

记 ${\displaystyle S(N)=\sum _{n=3}^{N}P(n)}$$\displaystyle S(N) = \sum_{n=3}^N P(n)$，已知 $S(10)=74$$S(10) = 74$。

求 $S(50)$$S(50)$。

点 这个链接 回到源站。

点 这个链接 回到详细版题目目录。