860. Gold and Silver Coin Game

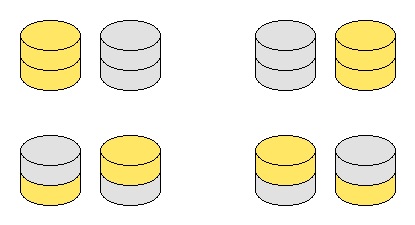
Gary and Sally play a game using gold and silver coins arranged into a number of vertical stacks, alternating turns. On Gary's turn he chooses a gold coin and removes it from the game along with any other coins sitting on top. Sally does the same on her turn by removing a silver coin. The first player unable to make a move loses.

An arrangement is called fair if the person moving first, whether it be Gary or Sally, will lose the game if both play optimally.

Define $F(n)$$F(n)$ to be the number of fair arrangements of $n$$n$ stacks, all of size $2$$2$. Different orderings of the stacks are to be counted separately, so $F(2)=4$$F(2) = 4$ due to the following four arrangements:

You are also given $F(10)=63594$$F(10) = 63594$.

Find $F(9898)$$F(9898)$. Give your answer modulo $989898989$$989898989$

860. 金币银币游戏

现将若干金币和银币垒成竖直的若干叠，加里和萨利正用这些硬币玩游戏，二人轮流操作。轮到加里时，他可以选择一枚金币，并将该金币与其上方的所有硬币移走。轮到萨利时，他可以选择一枚银币，并将该银币与其上方的所有硬币移走。首先无法操作者输。

如果二人都采取最优策略时，不论谁是先手，先手都必败，则称对应的初始局面是 公平的。

记：将 $2n$$2n$ 枚硬币垒成 $n$$n$ 个大小是 $2$$2$ 的堆，能产生 $F(n)$$F(n)$ 个公平的初始局面。这里，同样的 $n$$n$ 堆的不同排列须被计数多次。所以 $F(2)=4$$F(2) = 4$，$4$$4$ 种公平的初始局面如下图：

亦已知 $F(10)=63594$$F(10) = 63594$。

求 $F(9898)$$F(9898)$ 模 $989898989$$989898989$ 的值。

点 这个链接 回到源站。

点 这个链接 回到详细版题目目录。