846. Magic Bracelets

A bracelet is made by connecting at least three numbered beads in a circle. Each bead can only display $1$, $2$, or any number of the form $p^k$ or $2p^k$ for odd prime $p$.

In addition a magic bracelet must satisfy the following two conditions:

• no two beads display the same number
• the product of the numbers of any two adjacent beads is of the form $x^2+1$.

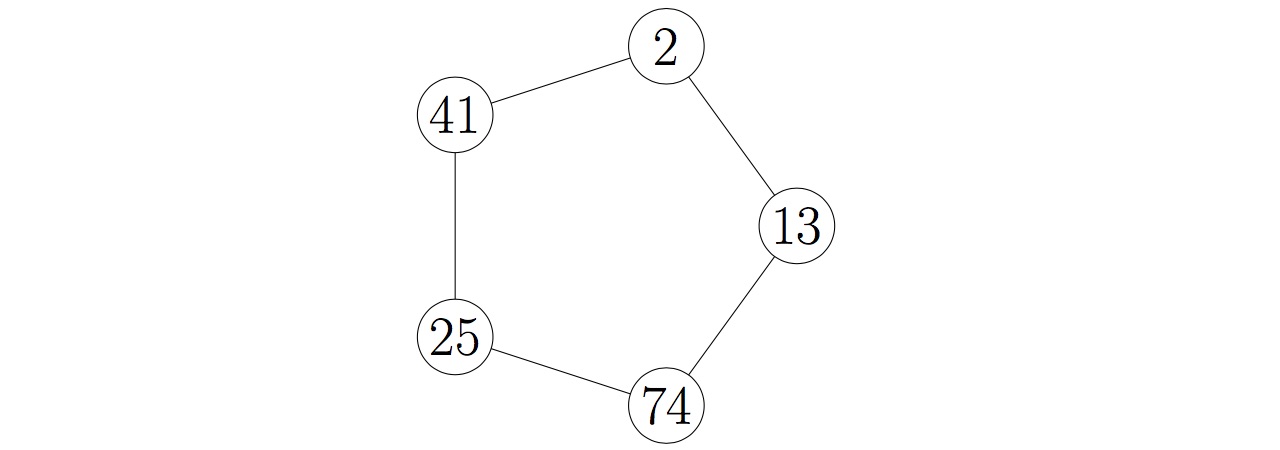
Define the potency of a magic bracelet to be the sum of numbers on its beads. The example is a magic bracelet with five beads which has a potency of 155.

Let $F(N)$ be the sum of the potency of each magic bracelet which can be formed using positive integers not exceeding $N$, where rotations and reflections of an arrangement are considered equivalent. You are given $F(20)=258$ and $F(10^2)=538768$.

Find $F(10^6)$.

846. 魔法数镯

一个数镯由至少三个标有数字的珠子和连接它们的环构成。数镯上的珠子的标号只能是 $1$、$2$、$p^k$、$2p^k$ 四种形式之一（其中 $p$ 为任意奇质数，$k$ 为任意正整数）。

进一步，定义魔法数镯为满足以下条件的数镯：

• 数镯上的珠子的标号两两不同。
• 任意两个相邻珠子上的标号之积均可被表示为 $x^2 + 1$ 的形式（其中 $x$ 为整数）。

对任意魔法数镯，定义其魔法效力为其所有珠子标号之和。上图中的魔法数镯共有 5 个珠子，魔法效力为 155。

记 $F(N)$ 为：满足所有珠子标号均为不超过 $N$ 的正整数的魔法数镯的魔法效力之和，其中，经旋转或翻转后相同的数镯视为相同的数镯。已知：$F(20) = 258$、$F(10^2) = 538768$。

求 $F(10^6)$。

点 这个链接 回到源站。

点 这个链接 回到详细版题目目录。