嘛貌似是远古时期写的文章了 qwq 填了填坑
玩过 Euclidea 吗?
啥?那个暴力搜索游戏?
玩这个游戏,你需要…
- 中学几何知识
- 会遐想
一个效率较好的暴力搜索程序
Alpha $\alpha$ 关(全解完成)
- 共计 11 关,4 个教程关,7 个主关
- 36 颗星,其中 V 星 3 个
Tutorial 等边三角形 / Equilateral Triangle(V 星关)
- 限制:4L 4E。解数:2
Construct an equilateral triangle with the given side. The construction must be exact. Guessing even very close points does not count as a solution.
过已知边作等边三角形。构造必须精确,即使猜的点非常接近也不被算为正解。
4L 4E 等腰三角形三边相等
- 工具:圆,圆,线,线
2V 下面还有一个
Alpha.1 60° 角 / Angle of 60° (V 星关)
- 限制:3L 3E。解数:2
Construct an angle of 60° with the given side.
过给定射线做一个 60° 角。
3L 3E 等价于上一关
- 工具:圆,圆,线
2V 下面还有一个
Tutorial 教程:相交工具 / Tutorial: Intersect Tool
- 限制:0L 0E。
… construct the intersection of the given circles.
求两圆交点。
0L 0E 点相交工具,再点两个圆就 OK
Alpha.2 垂直平分线 / Perpendicular Bisector
- 限制:3L 3E
Construct the perpendicular bisector of the segment.
作给定线段的垂直平分线。
3L 3E 初中基础尺规作图
- 工具:圆,圆,线
Tutorial 教程:垂直平分线 / Tutorial: Perpendicular Bisector
你可以直接点击线段的两个端点,作这个线段的垂直平分线了。使用花费:1L 3E
Alpha.3 中点 / Midpoint
- 限制:2L 4E
Construct the midpoint of the segment defined by two points.
作给定两点对应线段的中点。
2L 4E 1L3E 用中垂线,1L1E 连接两个端点,两条线的交点即为所求。
Alpha.4 正方形内的圆 / Circle in Square
- 限制:3L 5E
Inscribe a circle in the square.
在正方形内内接一个圆。
3L 5E 圆心:正方形对角线交点,半径:正方形边长一半,以此确定圆。
- 工具:中垂,线,圆
Tutorial 教程:移动 / Tutorial: Move Tool
这个描述的是帕斯卡定理。但你其实并不需要知道它是啥,随便拖着一个蓝点移动就 OK
Alpha.5 矩形内的菱形 / Rhombus in Rectangle(V 星关)
- 限制:3L 5E,解数:2
Inscribe a rhombus in the rectangle so that they share a diagonal.
在矩形内内接一个菱形,且二者共用一条对角线。
3L 5E 菱形对角线互相垂直平分,所以随便选一条对角线并作其垂直平分线。与矩形产生 2 个交点,加上选的那条对角线的顶点就有 4 个点了。注意其中标注的两条边已经有了别再画一遍…
2V 有两条对角线可选,就有两个不同菱形…
Alpha.6 圆心 / Circle Center
- 限制:2L 5E
Construct the center of the circle.Note! L and E goals are independent. To get 3 stars on this level you need to solve it twice: one solution with 2L and the other with 5E.
作给定圆的圆心。注意:本关 L 星,E 星为两个独立的任务。为了得到三星,你必须作图两次:一个 2L 的解和一个 5E 的解。
从这关开始,大多数关卡的 L 星,E 星都不能通过只作一次图同时得到。
2L 在圆上随便选两组点,作每组点的垂直平分线,交点即为中点
依据:垂径定理推论(弦的垂直平分线必经过圆心)
工具:中垂,中垂,交点
5E 利用共用圆的方法,作 3 个圆来得到 2 组垂直平分线,再求交点
- 工具:圆,圆,圆,线,线
Alpha.7 圆内接正方形 / Inscribed Square
- 要求:6L 7E
Inscribe a square in the circle. One vertex of the square is given.
以给定点为顶点,在圆中作一个内接正方形。
6L 直接连给定点与圆心得到正方形一条对角线,再做这个对角线的垂直平分线,四个顶点就都有了,顺次连接即可
- 依据:正方形对角线互相垂直平分
- 工具:线,中垂,线,线,线,线
7E 此任务是许多新手遇到的第一个障碍。故进行分步阐述
工具:圆,圆,线,线,线,线,线
第 1 步:以 A 为圆心,AO 为半径,作 $\bigodot A$,交原来的圆于 B、C
第 2 步:以 C 为圆心,CB 为半径,作 $\bigodot C$,交原来的圆于 D
结论 1:A、O、D 三点共线
证明: 首先可以清晰地看到 Tutorial 里的等边三角形模型,得 $\angle AOC=60^{\circ}$,运用圆周角定理可得 $\angle ABC=30^{\circ}$,易知 $\angle ACB=30^{\circ}$,$\angle BAC=120^{\circ}$。
然后有一个 SSS 全等:$\triangle ABC \cong \triangle ODC$,证明略去。于是 $\angle COD=120^{\circ}$,$\angle COD+\angle AOC=180^{\circ}$。得证!
- 第 3 步:以 O、C 为端点作直线,交 $\bigodot C$ 于 E、F
- 第 4~5 步:连接 D、E 交原来的圆于 G,连接 D,F 交原来的圆于 H
- 第 6~7 步:连接 AG,AH。
证明: 首先,由直径 $EF$ 的圆周角得出 $\angle EDF = 90^{\circ}$,直径 $AD$ 的圆周角得出 $\angle AGD = 90^{\circ}$,$\angle AHD = 90^{\circ}$,证明出 4 个 $90^{\circ}$。
上文已证出 $\angle COD = \angle DOC = 30^{\circ}$,圆周角定理得 $\angle EFD = 15^{\circ}$,进一步可得 $\angle CDF = 15^{\circ}$,$\angle ADH = 45^{\circ}$。此时就可以证明这是一个正方形了。
Beta $\beta$ 关(全解完成)
- 共计 12 关,2 个教程关,10 个主关
- 38 颗星,其中 V 星 2 个
Beta.1 角平分线 / Angle Bisector
- 限制:2L 4E
Construct the line that bisects the given angle.
作给定角的角平分线。
2L 4E 以任意半径作圆,这个圆与给定角有两个交点,作两个交点的垂直平分线即可。
- 依据:等腰三角形三线合一
- 工具:圆,中垂
Tutorial 教程:角平分线 / Tutorial: Angle Bisector
你可以顺次点击角一条边上的任意一点,角的顶点,角另外一条边上的任意一点,来直接画出这个角的角平分线了。花费:1L 4E
Beta.2 角平分线交点 / Intersection of Angle Bisectors
- 限制:2L 6E
Construct the point where the angle bisectors of the triangle are intersected.
作给定三角形三个角角平分线的交点。
2L 这就是内心… 只要做两个角的角平分线,取交点就可以了
- 工具:角分,角分,交点
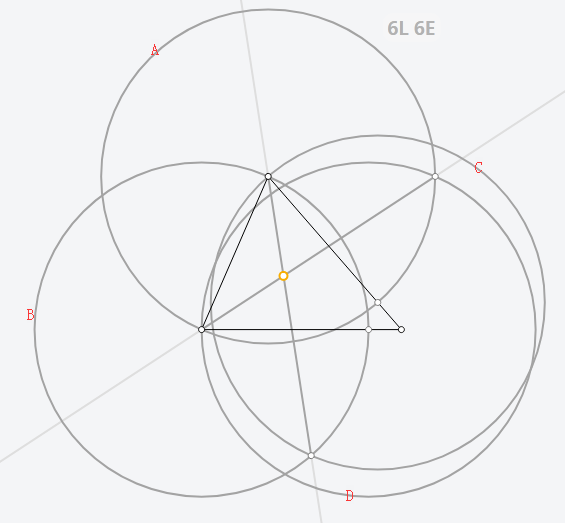
6E 巧妙地共用圆,用 4 个圆作两条角平分线。如图,A,B 两个圆被共用。
Beta.3 30° 角 / Angle of 30°(V 星关)
- 限制:3L 3E,解数:2
Construct an angle of 30° with the given side.
以给定射线为一边,作一个 30° 角。
3L 3E 先构造出 60° 角,再作 30° 角。
依据:圆周角定理
工具:圆,圆,线
2V 下面还有一个。
Beta.4 二倍角 / Double Angle(V 星关)
- 限制:3L 3E,解数:2
Construct an angle equal to the given one so that they share one side.
作一个与已知角相等的角,使它们有且只有一条公共边。
3L 3E 作圆后,构造二倍弧。
- 工具:圆,圆,线
2V 下面还有一解。
Beta.5 切割矩形 / Cut Rectangle
- 限制:3L 3E
Construct a line through the given point that cuts the rectangle into two parts of equal area.
过给定点引一条直线,使得这条直线平分矩形的面积
3L 3E
依据:过矩形中心的直线平分矩形面积。
工具:线,线,线
Beta.6 过线外一点作垂线 / Drop a Perpendicular
- 限制:2L 3E
Drop a perpendicular from the point to the line.
由给定点向直线引一条垂线。
2L
- 依据:垂径定理推论(弦的垂直平分线必经过圆心)
- 工具:圆,中垂
3E 作给定点对于给定直线的对称点,连接即可。
- 工具:圆,圆,线
Beta.7 过线上一点引垂线 / Erect a Perpendicular
- 限制:1L 3E
Erect a perpendicular from the point on the line.
由给定点向直线引一条垂线。
1L $180^{\circ} = 90^{\circ} \times 2$,等价于作角平分线。
- 工具:角分
3E 过给定点任意作圆,做出对应直径,即可得到垂线。
- 依据:直径所对圆周角为 $90^{\circ}$
- 工具:圆,线,线
Tutorial 教程:垂线 / Tutorial: Perpendicular
你可以直接过一点作一条直线的垂线了。花费:1L 3E
Beta.8 过圆上一点的切线 / Tangent to Circle at Point
- 限制:2L 3E
Construct a tangent to the circle at the given point.
在给定点上作给定圆的切线。
2L
- 依据:圆的切线垂直于过切点的半径
- 工具:圆,垂直
3E 分步解释
- 第 1 步:在 $\bigodot A$ 上任意选取异于 $B$ 的一点 $C$,以 $C$ 为圆心,$BC$ 长为半径作 $\bigodot C$,$\bigodot C$ 与 $\bigodot A$ 的另一个交点为 $D$
- 第 2 步:以 $B$ 为圆心,$BD$ 长为半径作 $\bigodot B$,$\bigodot C$ 与 $\bigodot B$ 的另一个交点为 $E$
- 第 3 步:连接 BE 即为所求。
证明
- 依据:弦切角逆定理(以三角形任意一条边为邻边,在三角形外部作一个角等于该边的对角,那么所作角的另一边与三角形外接圆相切,切点为所作角的顶点。)
由圆可以轻易推出 $DC = CB$,$CB = CE$,$DB=EB$。可得到 $\triangle DCB \cong \triangle BCE$,$\angle BDC = \angle CBE$。由弦切角逆定理,$BE$ 为 $\bigodot A$ 的切线,$B$ 为切点。
Beta.9 直线的切圆 / Circle Tangent to Line
- 限制:2L 4E
Construct a circle with the given center that is tangent to the given line.
给定圆心,作圆使得这个圆与给定直线相切。
2L 4E 说明略…
- 工具:垂直,圆
Beta.10 菱形的内切圆 / Сircle in Rhombus
- 限制:4L 6E
Inscribe a circle in the rhombus.
在菱形内内接一个圆。
4L 6E 连接两条对角线,作垂直获得切点,最后画圆就 OK
Gamma $\gamma$ 关(全解完成)
- 共计 9 关,全是主关
- 30 颗星,其中 V 星 3 个
Gamma.1 弦中点 / Chord Midpoint
- 限制:2L 4E
Construct a chord whose midpoint is given.
给定弦的中点,作弦。
2L 4E 连接两点,再作垂线。
- 依据:垂径定理
- 工具:线,垂直
Gamma.2 由角和垂心定义的三角形 / Triangle by Angle and Orthocenter
- 限制:3L 7E
Construct a segment connecting the sides of the angle to get a triangle whose orthocenter is in the point O.
作一条线段,使其连接已知角的两边,从而获得一个垂心为 O 的三角形。
3L 作垂得到另外两点的位置,连接即可。
- 依据:垂心的性质
- 工具:垂直,垂直,线
6E 与 3L 思想一样,用 Beta.6 3E 的方法作垂线,用共用圆的思想,使用 3 个圆作 2 条垂线。
- 依据:垂心的性质
- 工具:圆,圆,圆,线,线,线
Gamma.3 垂直平分线交点 / Intersection of Perpendicular Bisectors
- 限制:2L 2E
Construct a segment connecting the sides of the angle to get a triangle whose perpendicular bisectors are intersected in the point O.
作一条线段,使其连接已知角的两边,从而获得一个三边垂直平分线交点为 O 的三角形。
2L 2E 三边垂直平分线交点?就是外心啊!作出外接圆,连接交点就可以了
- 依据:外心到三角形三边的距离相等。
- 工具:圆,线
Gamma.4 三条等长线段 I / Three equal segments - 1(V 星关)
- 限制:4L 6E,解数:2
Given an angle ABC and a point M inside it, find points D on BA and E on BC and construct segments DM and ME such that BD = DM = ME.
给定 $\angle ABC$ 与在角内的一点 M,在射线 AB 上,射线 BC 上分别作出点 D、E,使得 BD = DM = ME
4L 6E 很明显 D 在 BM 垂直平分线上,E 一定在以 DM 为半径,M 为圆心的圆上
- 依据:垂直平分线的性质;圆的半径处处相等
- 工具:中垂,线,圆,线
2V 明显 $\bigodot M$ 与 BC 有两个交点,所以 E 点有 2 个
Gamma.5 过一点并切直线的圆 / Circle through Point Tangent to Line
- 限制:3L 6E
Construct a circle through the point A that is tangent to the given line at the point B.
构造一个圆,使其经过点 A,并与给定直线相切于点 B。
3L 作 AB 垂直平分线得到圆心所在直线。由于相切于 B,过 B 点作垂得到圆心,作圆即可。
- 工具:中垂,垂直,线
6E 运用共用圆思想,使用两个圆来同时达成作垂线与垂直平分线。如下图,作垂线用的是 Beta.7 3E 的做法。
- 工具:圆,圆,线,线,线,圆
Gamma.6 梯形底边的中点 / Midpoints of Trapezoid Bases
- 限制:3L 5E
Construct a line passing through the midpoints of the trapezoid bases.
做一条直线,使其经过梯形两条底边的中点。
3L 用垂直平分线作出两个中点,连接即可
- 工具:中垂,中垂,线
5E 详细证明见下
- 工具:线,线,线,线,线
证明
- 依据:边元塞瓦(Ceva)定理(在 $\triangle ABC$ 内任取一点 O,延长 AO、BO、CO 分别交对边于 D、E、F,则 $\frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB} = 1$)
首先可以轻易看出,把梯形补成三角形后,只要作出三角形中位线就可以了。
由梯形 $AB \parallel CD$,易得 $\frac{FA}{AC} = \frac{FB}{BD}$,即 $\frac{FA}{AC} \times \frac{BD}{FB} = 1$。
由塞瓦定理 $\frac{CG}{GD} \times \frac{FA}{AC} \times \frac{BD}{FB} = 1$,所以 $\frac{CG}{GD} = 1$,$CG = GD$。G 为 CD 中点。
故 EG 为三角形中位线。
注:由于博客 BUG,下文的所有图片无法显示。
Gamma.7 45° 角 / Angle of 45°
- 限制:2L 5E,解数:2
Construct an angle of 45° with the given side.
以给定射线为一边,做一个 45° 角。
2L 平分直角。
- 工具:垂,角分
5E 利用正方形一边与一条对角线构造 45°。
- 工具:圆,垂,线
2V 下面还有一个。
Gamma.8 菱形 / Lozenge
- 限制:5L 7E,解数:4
Construct a rhombus with the given side and an angle of 45° in a vertex.
以给定线段为一边,作一个顶角为 45° 的菱形。
5L 先构造出 45° 得到两边,作垂得到第三边,利用三点共线得到第四条边。
- 工具:圆,垂,角分,线,垂
7E 主体思想与 5E 基本相同。在 45° 构造上,7E 使用了 Gamma.7 4E 的方法。
- 工具:圆,圆,线,圆,线,线,线
4V 上、下两类;顶角顶点有 2 个;共 4 个可能的菱形。
Gamma.9 四边形的中心 / Center of Quadrilateral
- 限制:4L 10E
Construct the midpoint of the segment that connects the midpoints of the diagonals of the quadrilateral.
构造出四边形两对角线所连线段的中点。
4L 10E 任意选取四边形一条边,再选取一条对边,作这两条边的中点并连接,该线段的中点即为所求。
- 工具:中垂,中垂,线,中垂
证明
待补。
Delta $\delta$ 关
- 共计 10 关,全是主关
- 34 颗星,其中 V 星 4 个
Delta.1 二倍线段 / Double Segment
- 限制:3L 3E,解数:2
Construct a point C on the line AB such that |AC|=2|AB| using only a compass.
仅用圆规,作出满足 $|AC| = 2|AB|$ 的点 $C$。
3L 3E 在 Alpha.7 关中已有证明,此处不再赘述。
- 工具:圆,圆,圆
2V 左右各有一个。
Delta.2 60° 角 - 2 / Angle of 60° - 2
- 限制:3L 4E,解数:2
Construct a straight line through the given point that makes an angle of 60° with the given line.
过给定点做直线,使得该直线与给定直线成 60° 角。
3L 见图。证明比较容易,只需注意到 60° 模型应该就不难了。
- 依据:圆周角为圆心角一半,垂径定理逆定理
- 步骤:圆,圆,中垂
4E 见图。
- 步骤:圆,圆,圆,线
证明
Epsilon $\varepsilon$ 关
- 共计 12 关,1 个教程关,11 个主关
- 40 颗星,其中 V 星 4 个
咕咕咕…
6、$\zeta$ Zeta 关
- 共计 12 关,1 个教程关,11 个主关
- 41 颗星,其中 V 星 5 个
咕咕咕…
7、$\eta$ Eta 关
- 共计 11 关,全是主关
- 37 颗星,其中 V 星 4 个
咕咕咕…
8、$\theta$ Theta 关
- 共计 7 关,全是主关
- 27 颗星,其中 V 星 6 个
咕咕咕…
9、$\iota$ Iota 关
- 共计 10 关,全是主关
- 32 颗星,其中 V 星 2 个
咕咕咕…
10、$\kappa$ Kappa 关
- 共计 12 关,全是主关
- 42 颗星,其中 V 星 6 个
咕咕咕…
11、$\lambda$ Lambda 关
- 共计 10 关,全是主关
- 34 颗星,其中 V 星 4 个
咕咕咕…
12、$\mu$ Mu 关
- 共计 10 关,全是主关
- 35 颗星,其中 V 星 5 个
咕咕咕…
13、$\nu$ Nu 关
- 共计 9 关,全是主关
- 34 颗星,其中 V 星 7 个
咕咕咕…
14、$\xi$ Xi 关
- 共计 5 关,全是主关
- 19 颗星,其中 V 星 4 个
咕咕咕…
15、$\omicron$ Omicron 关
- 共计 11 关,全是主关
- 37 颗星,其中 V 星 4 个
咕咕咕…